Писания предсказывают
§ 13. Математика и глобальная научно-техническая революция.
Развитие классической механики и развитие квантовой механики в истории человеческой цивилизации дважды определили научно-техническую революцию. И каждый раз математике принадлежала главенствующая роль.
Классическая и квантовая механики практически исчерпали свои основные возможности. Основой грядущей глобальной научно-технической революции станет незримая механика и в ее постижении, после «Ла илаха иль Аллах», опять главенствующую роль будет играть математика.
Попробуем это доказать. Вкратце изложим известные понятия.
1. Натуральные числа. Числа 1,2,3,4,5, …, использующиеся для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов, называются натуральными. Любое натуральное число в десятичной системе исчисления записывается с помощью цифр 1,2,3,4,5,6,7,8,9 и знака 0.
Проведем прямую L , отметим на ней точку О, которую примем за начало отсчета, выберем направление и единичный отрезок [0;1]
_ А 1____________________________________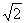 А А

_-3 ____________0_____ 1 _____________3 p L
Рис.1
В этом случае говорят, что задана координатная прямая. Каждому натуральному числу соответствует одна точка прямой L . Пусть, например, дано число 3. Отложим от точки О в заданном направлении единичный отрезок три раза, получим точку А – эта точка и соответствует числу 3.
В области натуральных чисел всегда выполнимы только сложение и умножение. Вычитание уже может приводить к другим числам.
2. Отрицательные числа. Отложим теперь три раза единичный отрезок от точки О в направлении, противоположном заданному. Получим точку А 1, симметричную точке А относительно начала отсчета О. Координатой точки А является число 3, а координатой точки А 1 является число минус три, записывают так: «-3» и читают: «минус 3». Числа 3 и -3 называют противоположными. Числа, которым соответствуют точки, расположенные на координатной прямой в направлении, противоположном заданному, называют отрицательными.
3. Целые числа. Натуральные числа 1,2,3,4,5,6 … и числа, им противоположные -1,-2,-3,-4,-5, … называют целыми числами. Знак 0 также считают целым числом. Итак, целые числа – это натуральные числа, числа, противоположные натуральным, и число 0. В области целых чисел выполнимы только три арифметических действия: сложение, умножение и вычитание. Деление не всегда выполнимо в области целых чисел и приводит к дробным числам.
4. Рациональные числа. Целые числа и дроби (положительные и отрицательные) составляют вместе множество рациональных чисел. Любое рациональное число может быть представлено в виде отношения 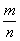 , где m – целое число, а n – натуральное число. В области рациональных чисел всегда выполнимы все четыре действия арифметики, но действие извлечения корня не всегда возможно. , где m – целое число, а n – натуральное число. В области рациональных чисел всегда выполнимы все четыре действия арифметики, но действие извлечения корня не всегда возможно.
5.Иррациональные числа. Задачи измерения непрерывных величин, то есть выражения всякого значения такой величины числом, привели к введению чисел иррациональных.
Историческое предание приписывает так называемое «открытие» иррациональных чисел Пифагору, который обнаружил несоизмеримость диагонали квадрата с его стороной. То есть, если сторону квадрата принять за единицу, то длина диагонали квадрата не может быть выражена никаким рациональным числом – длина диагонали может быть выражена только бесконечной дробью: 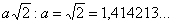 . Это число иррациональное. . Это число иррациональное.
Решение многих других задач так же приводят к иррациональным числам. Например, число 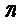 , выражающее отношение длины окружности к диаметру нельзя представить в виде обыкновенной дроби – это иррациональное число. , выражающее отношение длины окружности к диаметру нельзя представить в виде обыкновенной дроби – это иррациональное число.
6. Действительные числа. Рациональные и иррациональные числа составляют вместе множество действительных чисел. Каждому действительному числу соответствует единственная точка координатной прямой. Каждая точка координатной прямой соответствует единственному действительному числу.
Множество действительных чисел упорядочено. То есть, для любых неравных действительных чисел a и b можно сказать, какое больше, а какое меньше.
Говорят, что число a больше числа b , если разность a - b – положительное число; если же a – b отрицательное число, то говорят, что число a меньше числа b .
7. Комплексные числа. Не успело еще закрепиться новое расширенное понятие числа, как в процессе дальнейшего развития математики обнаружилось, что и новое понятие является так же неудовлетворительным. В частности, решение квадратных уравнений уже на самой ранней стадии развития алгебры привело к невозможной в области действительных чисел операции извлечения квадратного корня из отрицательного числа.
Величина b 2 при любом числовом значении b будет не отрицательна, то есть она может быть либо положительна, либо равна нулю, например при 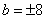 имеем имеем 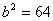 ; при b = 0 и b 2 = 0. ; при b = 0 и b 2 = 0.
Таким образом, среди действительных чисел нет ни одного такого, квадрат которого был бы величиной отрицательной; следовательно, и корень квадратный из отрицательной величины 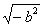 не может быть выражен никаким действительным числом. не может быть выражен никаким действительным числом.
Означает ли это, однако, что величина 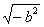 является «воображаемой», «невозможной», «мнимой», как ее называли, следуя традиции, неизменно повторяющейся при всяком новом расширении понятия числа? является «воображаемой», «невозможной», «мнимой», как ее называли, следуя традиции, неизменно повторяющейся при всяком новом расширении понятия числа?
Конечно, нет. Величина  является реально существующей величиной, которая только не может быть выражена узким, несовременным понятием действительного числа. является реально существующей величиной, которая только не может быть выражена узким, несовременным понятием действительного числа.
С аналогичным явлением мы сталкивались не только в математике. Например, обыкновенная фотопленка всю красочность природы передает как комбинацию черных и белых тонов. Однако в связи с этим никто не утверждает, что «действительным» цветом являются только белый и черный, а все остальные - «воображаемые», «невозможные», «мнимые». Новая, более современная пленка, светочувствительный слой которой состоит не из одного, а из трех слоев, чувствительных соответственно к синему, желтому и зеленому цветам, уже в состоянии дать снимок в натуральных красках.
Так и в рассматриваемом случае, кроме известной «действительной» единицы, при помощи которой выражаются все «действительные числа», необходимо ввести еще одну, принципиально новую единицу, которую будем обозначать буквой i , понимая под этим обозначением величину
 или или 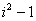 . (5.1) . (5.1)
Тогда 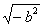 может быть выражено через новую единицу i так: может быть выражено через новую единицу i так:
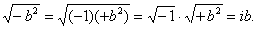 (5.2). (5.2).
По исторической традиции число i назвали мнимой единицей, а числа ib – чисто мнимыми числами.
Числа вида a + ib получили название комплексного числа в котором различают действительную часть ( a ) и мнимую часть ( b ).
Действительные числа, как было сказано выше, геометрически изображаются точками числовой оси. Комплексные числа на одной числовой оси представить невозможно. Они изображаются точками числовой плоскости: каждое конкретное комплексное число изображается точкой в системе прямоугольных координат. Осью абсцисс является действительная числовая ось, а осью ординат – ось «чисто мнимых чисел».
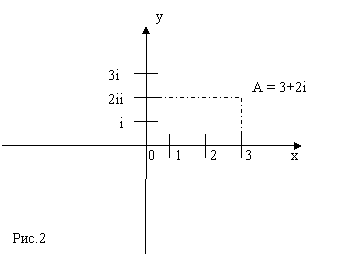 Для изображения комплексных чисел на числовой плоскости необходимо уже задать начало отсчета (нулевую точку), положительное направление каждой из осей и две масштабные единицы: действительную (1) и мнимую ( i ). Для изображения комплексных чисел на числовой плоскости необходимо уже задать начало отсчета (нулевую точку), положительное направление каждой из осей и две масштабные единицы: действительную (1) и мнимую ( i ).
Например, точка А на рисунке изображает комплексное число
А = 3+2 i
Установленный факт формулируется так: между точками числовой плоскости и всем множеством комплексных чисел существует взаимно однозначное соответствие. В случае в = 0 комплексное число обращается в число действительное, при 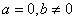 оно будет чисто мнимым. оно будет чисто мнимым.
Комплексные числа начали появляться в работах отдельных математиков начиная с XVI века. Но широкое признание и распространение они получили лишь в XIX веке, после того как на рубеже XVIII – XIX веков одновременно и независимо друг от друга К.Гаусом (в 1797- 1799 г.г.), К.Весселом (в 1798- 1799 г.г.), Ж.Арганом (в 1806 г.) была дана геометрическая интерпретация комплексных чисел как точек числовой плоскости, и после того как при помощи комплексных чисел удалось решить ряд практических важных задач, неразрешенных в области действительных чисел.
До тех пор к комплексным числам относились с большим недоверием и не понимали и сути даже многие крупные математики. Например, Лейбниц писал: «Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием».
Теперь из Корана приведем слова Господа Бога: «Это Писание, несомненно, наставление для тех, кто страшится гнева Бога и в незримое уверил,…». (С.2:2-5). Выходит, математики, с присущей им точностью, доказали существование параллельных миров, подтвердив тем самым еще раз, что Коран воистину справочник всего сущего.
Еще более поразительны в сличении с Кораном результаты математического предмета: «Теория функции комплексной переменной».
Например, в области комплексного переменного алгебраическое уравнение n -ой степени всегда имеет точно n корней, в то время как в области действительного переменного оно может иметь и меньшее число корней и даже ни одного.
В области комплексного переменного существует логарифм от отрицательных чисел, функции синус и косинус могут принимать любые значения, а не только значения, не превышающие единицы и т.д. (доказательства приводятся в любом учебнике по Теории функции комплексной переменной).
Это математическое доказательство участия незримой механики в реальных событиях, так как уравнения n -ой степени, логарифмические и тригонометрические функции – описание законов реальной жизни. Кроме того, это научное подтверждении е аята: «На небе ваши жизненные потребности и то, что вам обещано. Поэтому, клянусь Господом неба и земли, что это истина, такая же, что вы обладаете даром речи и разумно обращаетесь друг к другу». (С.51:22, 23).
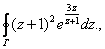
Рассмотрим еще два примера:
Пример 1. Вычислить интеграл где Г – окружность | Z +1| = 1, проходимая в положительном направлении.
Изолированной особой точкой подынтегральной функции является Z 0 = –1. Разложение этой функции в ряд Лоренца имеет вид:
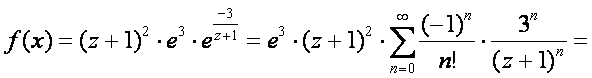
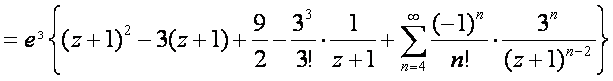  
Правильная часть Главная часть
Так как главная часть ряда Лорена представляет собой бесконечный ряд, то Z 0 = -1есть существенно особая точка f ( z ).
Находим вычет в этой точке:
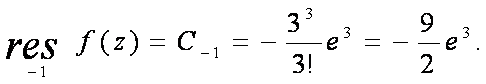
Согласно основной теореме о вычетах, имеем

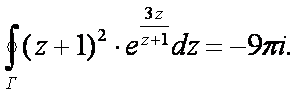 То есть: То есть:
Это значит, что сумма некоторой функции (некоторых действий) действительного аргумента по замкнутому контуру равна мнимому числу, то есть сумма (результат) некоторых действий в этом реальном мире переходит в параллельный мир.
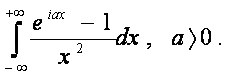
Пример 2. Вычислить интеграл
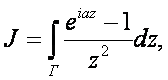
Рассмотрим интеграл где замкнутый контур
Г= γ 1 + γ 2 + γ 3 + γ 4 .
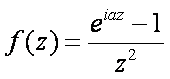 Внутри этого контура подынтегральная функция является аналитической и в силу интегральной теоремы Коши J =0. Внутри этого контура подынтегральная функция является аналитической и в силу интегральной теоремы Коши J =0.
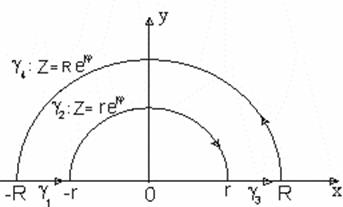
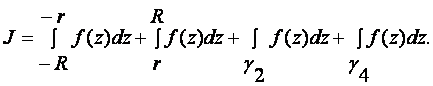
С другой стороны
При r = 0, R ® ¥ получим
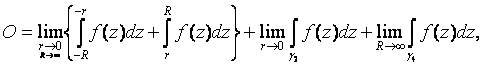
Откуда 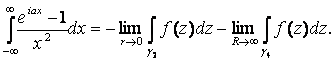
Второй предел равен нулю, так как | f ( z )| ~ 1/ R 2 при a >0 и R ® ¥ .
Для вычисления первого предела разложим экспоненту в ряд:
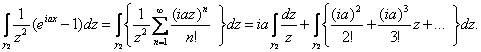
Второй интеграл, взятый по кривой γ 2 : z = re i j , стремится к нулю при r ® 0, а первый интеграл вычислим непосредственно:

Таким образом, исходный интеграл
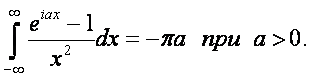
Для a <0, взяв в качестве Г контур внешней полуплоскости аналогично получим p a . Итак, окончательно находим
 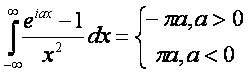
Итак, результат некоторой функции по мнимому аргументу равна действительному числу. Значит, результат некоторых действий в параллельном мире переходит в этот мир. То есть, параллельные миры непрерывно общаются и обмениваются по законам, описываемым математическими формулами.
Если Бог, человеку откроет этот математический закон, то человек может общаться с параллельным миром и пользоваться незримой механикой. Да простит и помилует нас Бог!
В резюме изложенного приведем уже известные законы незримой механики.
Первый закон : (основной закон) незримой механики: Ла илаха иль Аллах!
Если индивидуум непрерывно упоминает этот закон, получает индивидуальную долю незримой механики. Если общество людей упоминает этот закон непрерывно, получает общественную долю незримой механики. Государство, граждане которого более ближе к законам Создателя, выходят вперед в техническом и в экономическом развитии.
Второй закон незримой механики следует из
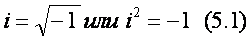
Если на незримое действие воздействовать незримым же действием такой же силы, будет реальный отрицательный результат и возведенный в квадрат по модулю. Поэтому незримым действиям не следует противодействовать. От них нужно искать убежище у Господа Бога.
Третий закон незримой механики: можно проследить на числовой плоскости (рис.2): все измерения классической и квантовой механики, выраженные в числах, умещается на одной числовой прямой. На числовой же плоскости, заполненной точками, соответствующими измерениям в мнимой механике, таких прямых бесконечно много. Следовательно, возможности незримой механики бесконечны и бесконечное число раз превышают возможности классической и квантовой механики вместе взятые.
Четвертый закон незримой механики: Исчерпанная возможность в классической и квантовой механике не означает исчерпанную возможность в незримой механике.
Пятый закон незримой механики проявляется на примерах 1 и 2: Классическая механика, квантовая механика и незримая механика неразделимы, работают совместно и дополняют друг друга.
Дальнейший вклад математики в освоение незримой механики, предпочтительно будет проходить по следующим направлениям: возрастание интересов и действий по изучению теории функции комплексного переменного; непрерывное сличение достигнутых математических результатов с аятами в Коране; математическая обработка законов и примеров, поступающих от физиков, химиков, биологов, медиков, социологов, историков, юристов и ученых других направлений; упорядочение поля комплексных чисел: и изучение (с физиками) участия функции комплексных переменных в разрешении задач в поле действительных чисел.
Множество комплексных чисел до сих пор не упорядочено по трем причинам: никто этим не занимался; практической потребности в этом не было; отсутствовала техническая возможность – получались очень громоздкие вычисления, которые вручную производить было невозможно. Сейчас ситуация изменилась: можно предположить, что в основном прогресс наук будет проходить через функции комплексных переменных; мощные компьютеры облегчают вычисления. Многовероятно, что математики интенсивно будут заниматься упорядочением и изучением комплексных чисел.
Приведем пример упорядочения множества комплексных чисел.
На числовой плоскости xOy обозначим комплексное число
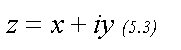
Вектор 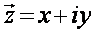 можно определить не только прямоугольными координатами X и Y ; его можно определить и полярными координатами: длиной вектора r и углом j , который вектор z образует с положительным направлением оси (рис.4). можно определить не только прямоугольными координатами X и Y ; его можно определить и полярными координатами: длиной вектора r и углом j , который вектор z образует с положительным направлением оси (рис.4).
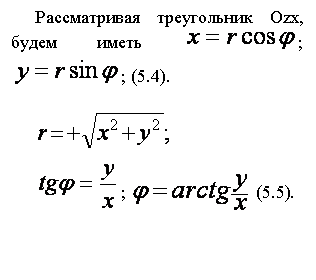

Положительное число r называется модулем, а угол j аргументом комплексного числа 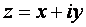 и обозначается и обозначается 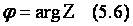
Зная, что х = r · cos j , у = rsin j можем комплексное число Z = x + i у представить в следующей форме:
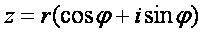 (5.7). (5.7).
Эта форма комплексного числа называется тригонометрической, форма (5.3) называется алгебраической.
Теперь на числовую плоскость наложим спираль Архимеда, как показано на рис.4 и введем определение.
Определение : Из двух комплексных чисел то больше, у которого модуль больше. При равенстве модулей двух комплексных чисел то комплексное число больше, у которого аргумент больше. Два комплексных числа равны тогда и только тогда, когда в отдельности равны их модули и аргументы.
Такое упорядочение комплексных чисел позволит в действующей теории комплексных переменных избежать введение не очень гладких понятий круговой (и другой) окрестности точки и о дополнении плоскости бесконечно удаленной точкой, а так же функции комплексных аргументов рассматривать по тем же правилам, что и функции действительных аргументов.
Математическая задача отображает некий физический процесс, ее
решение – результат процесса, ход решения – течение процесса. И если в ход решения математической задачи включаются функции с мнимыми аргументами, а затем до конца решения они исчезают, это значит, что в физический процесс включаются силы параллельных миров, создают результат и уходят, не фигурируя в конечном результате. Это еще одна из отправных точек в изучении и познании законов параллельных миров.
В теории функций комплексного переменного решаются задачи: нахождения аналитической функции по ее действительной части; нахождение аналитической функции по ее мнимой части; нахождение действительной или мнимой частей заданной аналитической функции. асширение, углубление и классификация решений этих задач – следующая отправная точка в изучении законов незримой механики.
Изложенное является схематичной научной программой многих десятков тысяч математиков на несколько столетий. В то же время эта программа очень конкретна: каждый день каждого математика можно планировать на конкретную задачу, которая будет давать конкретные реальные результаты.
|
